这篇我们讲另一种现代投资组合策略——均值方差(mean variance portfolio)。之前我们都是从风险的角度考虑去配置资产,均值方差则不同,其是从收益率的角度出发,给定一个收益率目标,从有效边界中找出一个风险最低的配置。
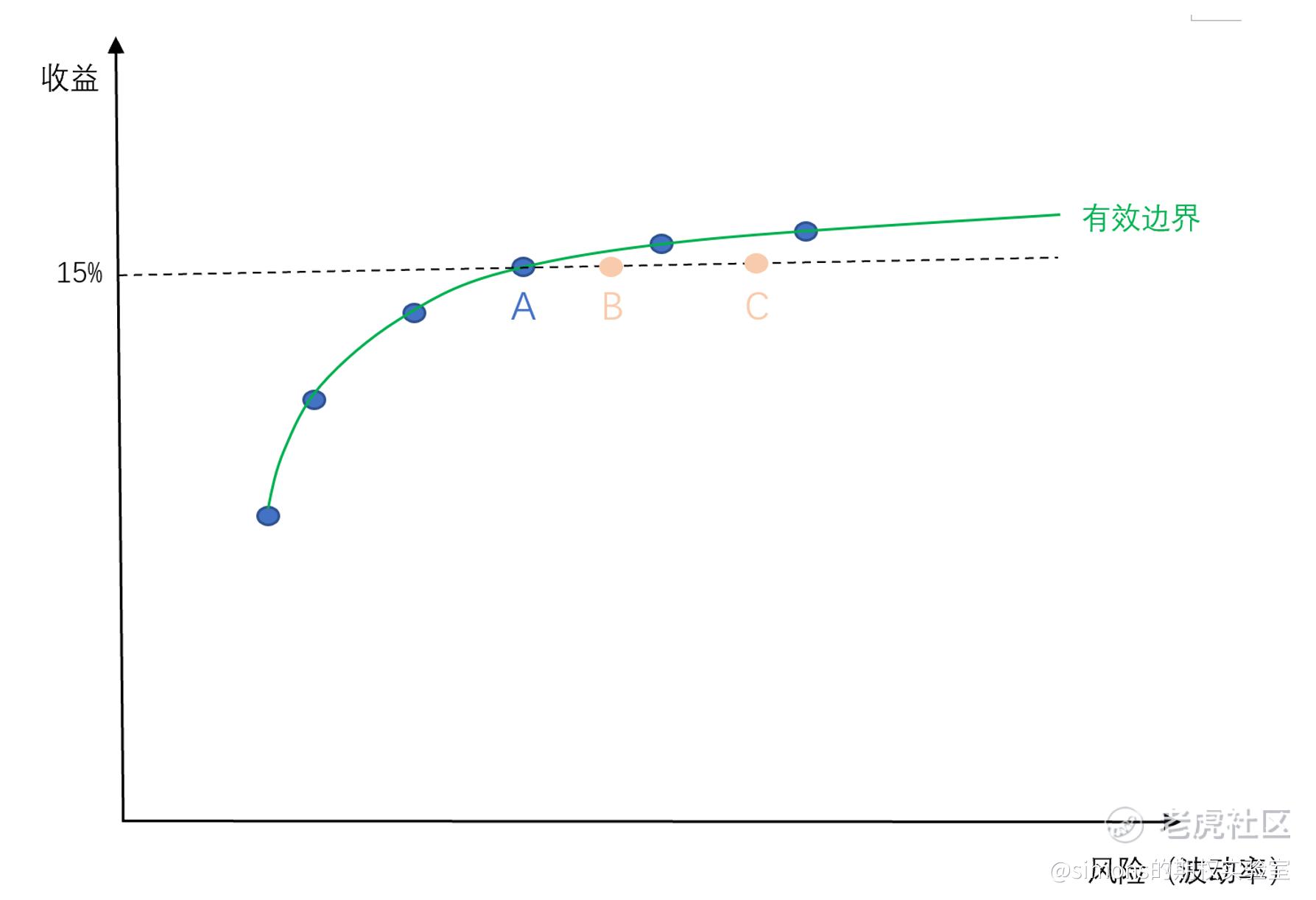
如上图,我们想从一堆资产组合中找到1种能达到15%的年收益的组合。我们从纵坐标15%的刻度位置向右拉一条水平线,其与有效边界交叉的A点即为我们要寻找的组合。B点、C点的收益虽然也能达到15%,但是风险都比A点高,不考虑。
我们继续以这16个ETF作为股票池来构建组合,规则是每种ETF持有一定百分比(0%-100%,0%就是不持有),也没有最低持有要求。在此规则下来找出能达到15%的收益率并且是风险最低的组合。这时候如果我们像之前用穷举法是不可能的,因为有亿万种组合可能。但是我们用专业的计算工具就能达到。
下图是这16个ETF的有效边界图。15%的有效边界点显示组合为:23.56%XBI、53.44%VGT、23%TLT。对的,只有3种ETF的配置,其余ETF没有入围这个风险最低的组合。通过计算机计算,这种组合能达到15%的收益且风险最低。
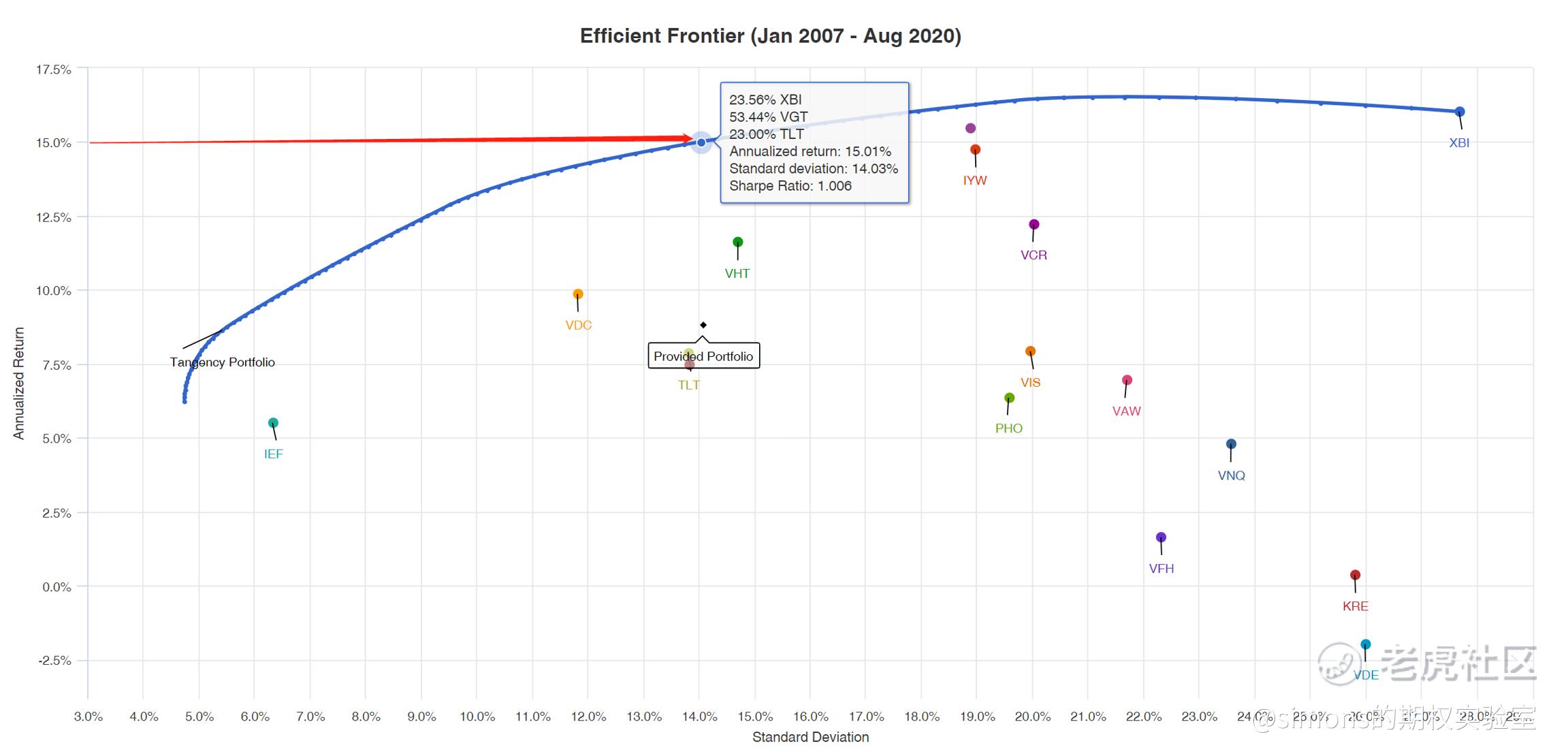
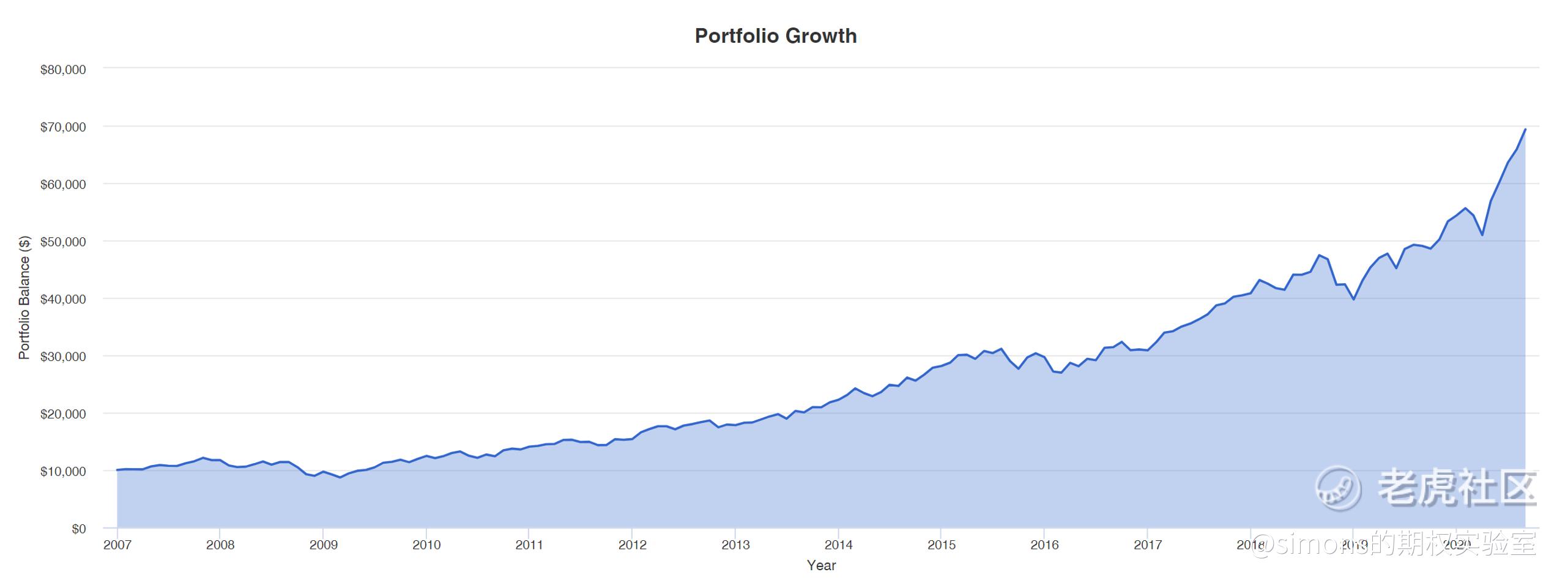
接下来我们用工具回测这个组合:
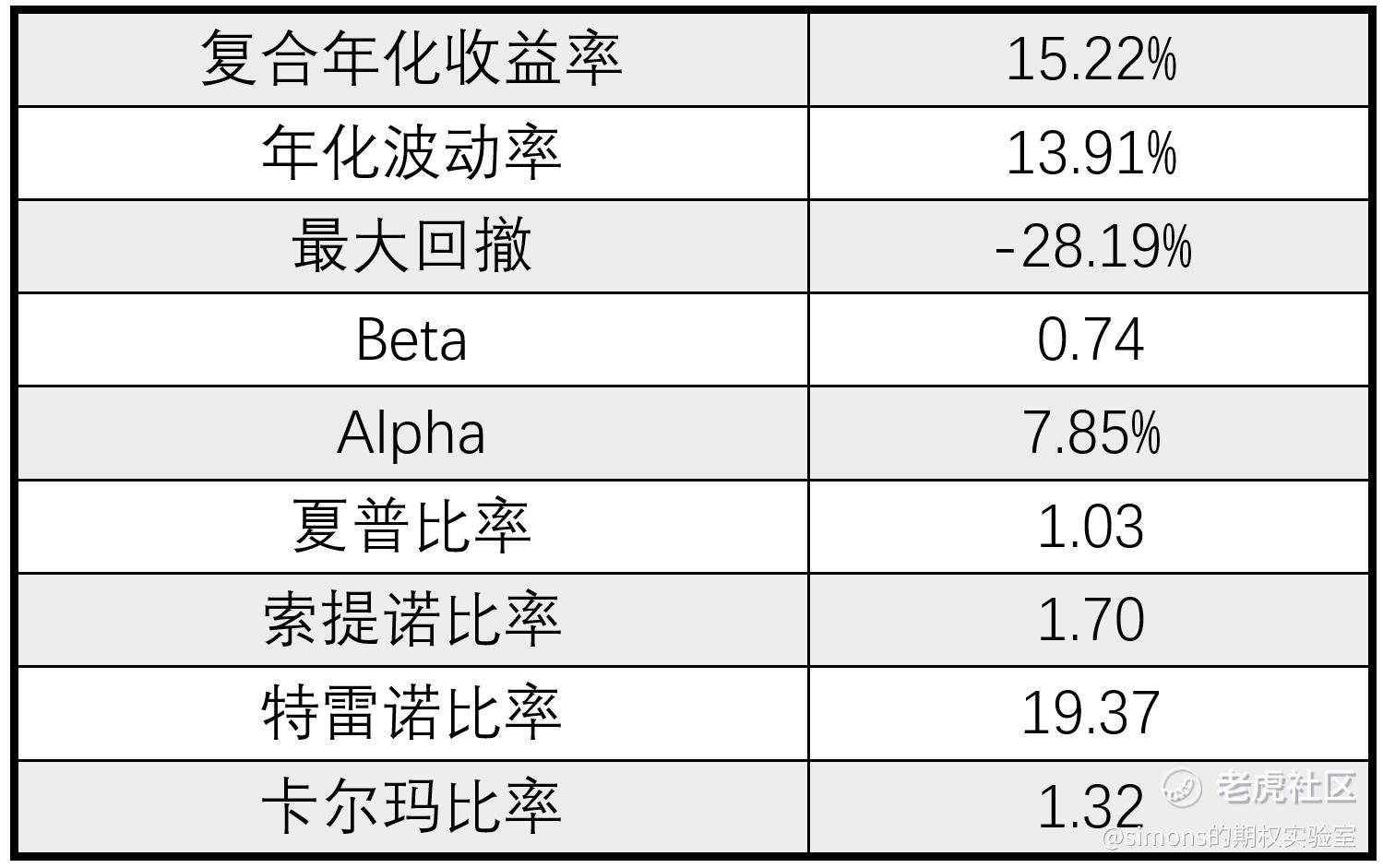
均值方差和最小方差是对冲基金使用的2种基本策略,不要走开,后面还有更多更精彩的策略和组合等着你。
未经允许不得转载:海外华人美股开户 » 现代资产组合论(四)——均值方差
 海外华人美股开户
海外华人美股开户