我们用有效边界的图继续,今天的主题是最低方差(minimum variance)。最低方差是一种组合的形式,也可以作为一种操作策略,广泛被对冲基金使用。
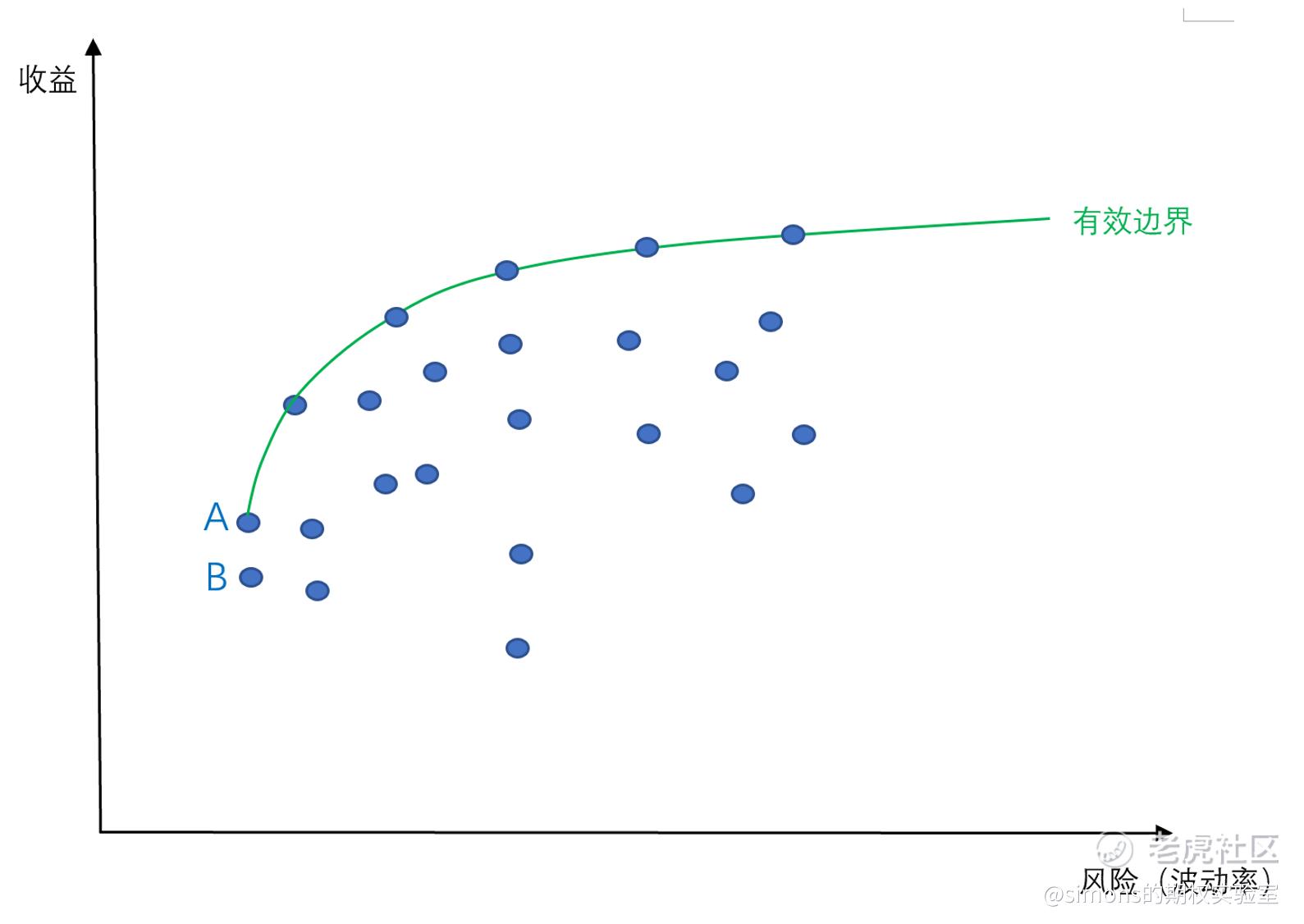
在读懂你的收益率曲线(五)——方差内,我们了解了方差的概念和计算过程。方差是波动率的平方,衡量着资产的风险。最低方差就是找出风险最低的投资组合。在有效边界图内,找出来很简单,最小的方差就是最小的波动率,也就是横坐标值最小的2个点:A点和B点。
现在有一个问题:选A还是选B?答案是一边倒的,肯定是A。因为A的收益比B高。没人会在承担相同的风险下,选择收益小的组合。同时A必然也落在有效边界上,为该弧线最左侧的一个点。
在对冲基金有一种时序模型(Timing Model)叫适应分配(Adaptive Allocation),原理是挑选一揽子资产或者股票,类似于自选股票池,然后用最小方差来挑选资产或股票,并每隔一定周期(比如每月)调整仓位。这种策略会制造出风险极低、收益稳定的资产收益曲线。
接下来我们用最小方差来做实验,选取16种ETF:
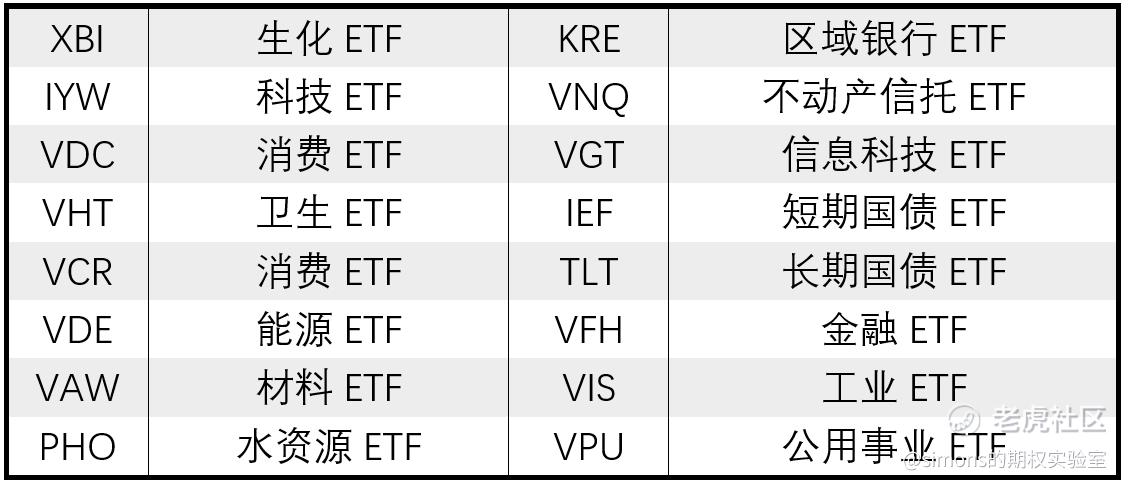
1、从上述16只ETF中用相对强度动量(relative strength momentum)选取表现最好的10只ETF。
2、记录过去3个月内的日波动率,用Minimum variance模型计算出10只ETF在达到某种配比后能得到最小收益率方差的组合。
3、每月的1号进行重新计算2、3并调仓。
4、所得到收益曲线如图(自2008年)。
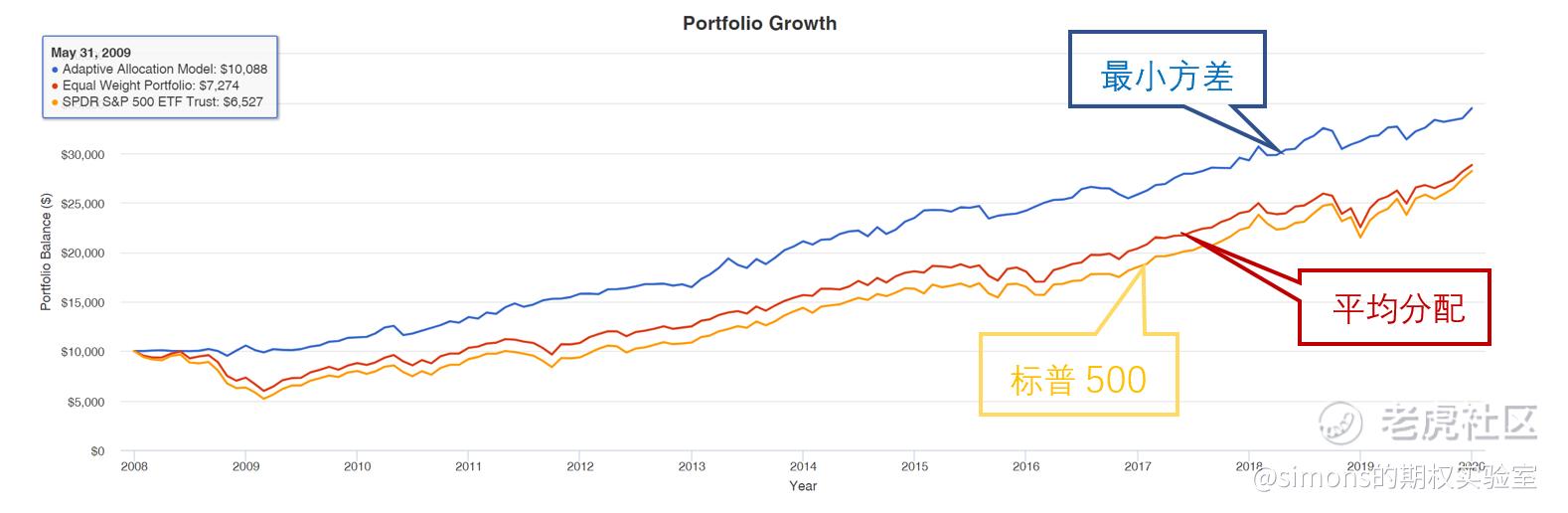
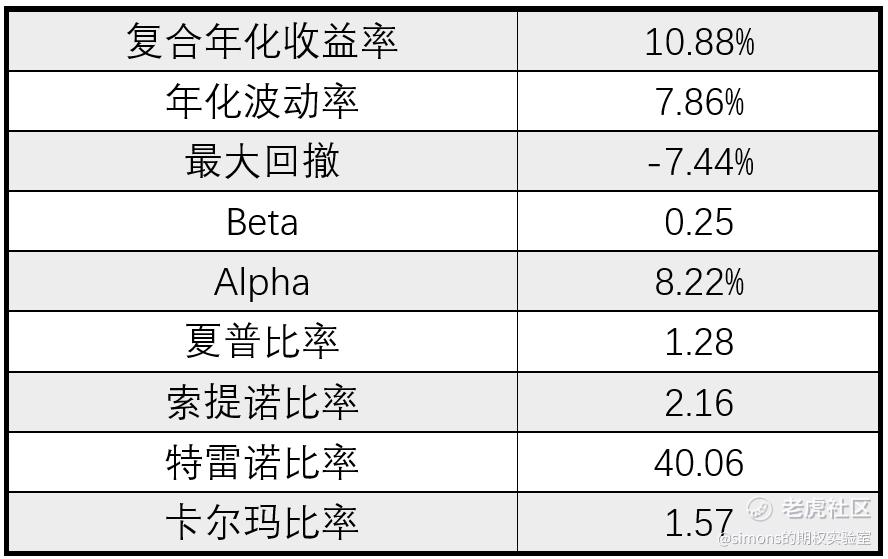
“最小方差组合”持续稳定地跑赢了大盘,12年间的最大回撤只有7%,beta只有0.25,也就是说系统性风险很低。我觉得最牛之处就是看曲线2008年次贷危机期间竟然没有回撤。11%的复合年化可以秒杀很多债基。
这种策略的组合适合保守的投资者,或者做保证金交易的,账户上有闲置现金的,都可以采用该策略进行低风险投资。
未经允许不得转载:海外华人美股开户 » 现代资产组合论(三)——最低方差
 海外华人美股开户
海外华人美股开户