tiger trade在前一篇内的最后我们举了一个资产配置的实例，一年前我们将账户内一半的资金买入SPY，一半的资金买入TLT。一年后的今天实现了24%的收益，更重要的是夏普比率达到2.0以上，秒杀了很多专业基金，看上去似乎不错。那有朋友会问：为什么要50%50%那么分呢？我觉得股市比债市好，股票60%国债40%，表现将如何呢？
我们用数据说话。用穷举法，按照不同的比例，一个一个去回测就清楚了，如下表：
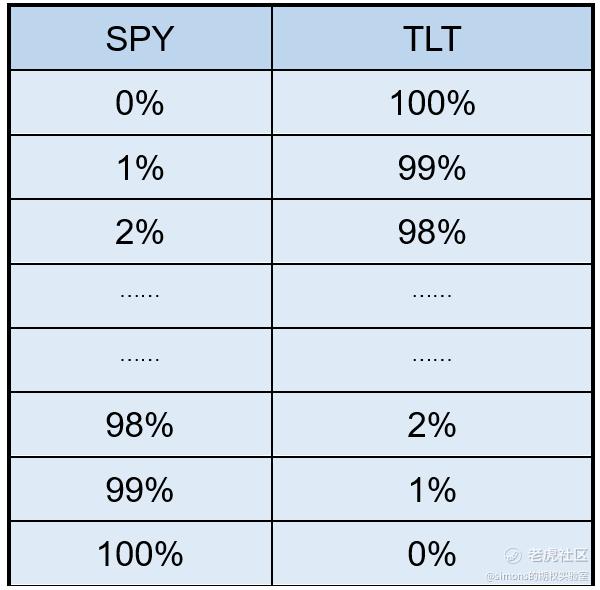
一共101种可能，回测产生了101条资产收益曲线，每条曲线（每一种比例）对应有1个收益率，1个波动率。
我们画一张坐标系，纵坐标为收益率，横坐标为波动率，每条条曲线的收益率和波动率，在图上都可以确定一个点，共计101个点，如下图：
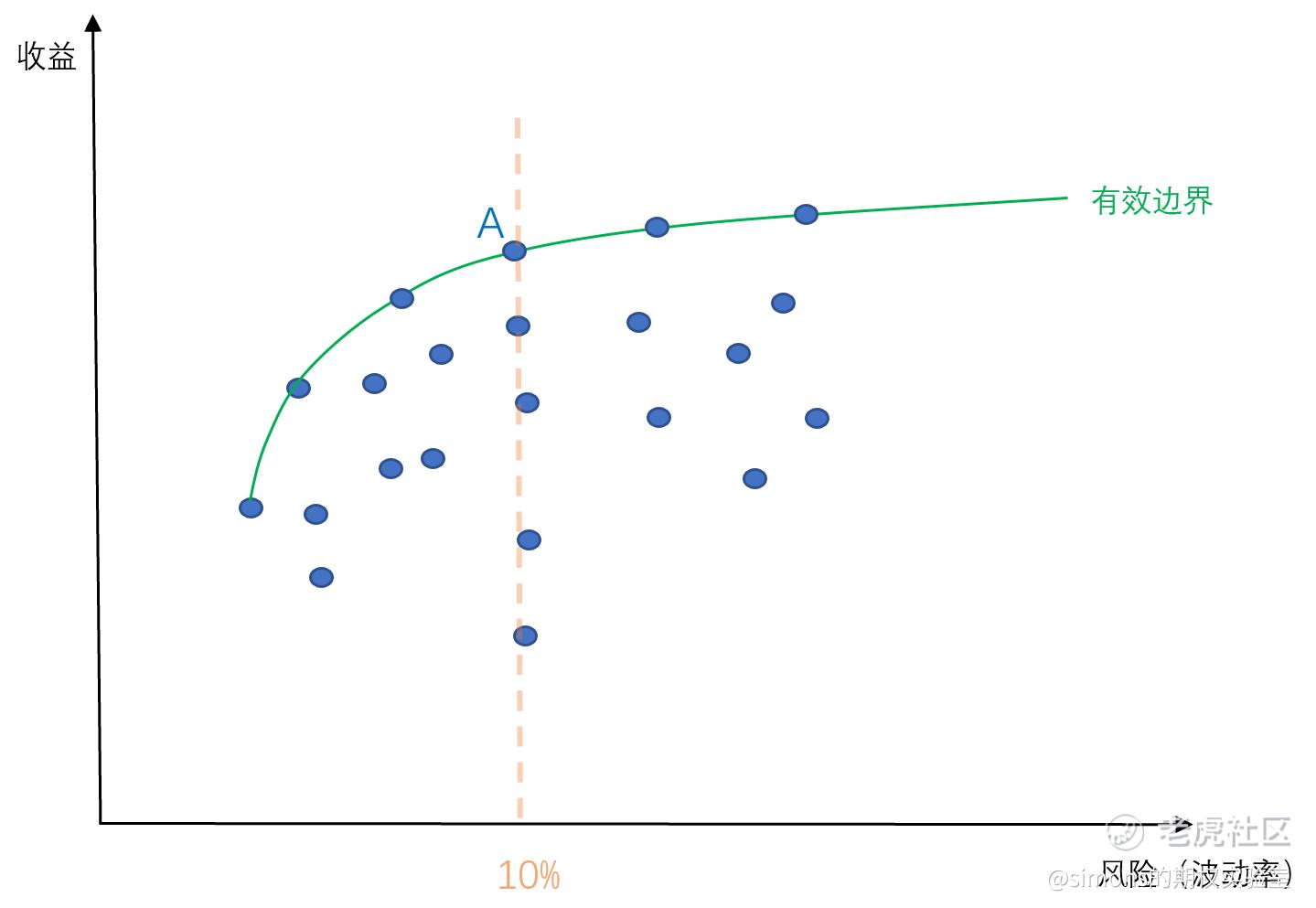
先来看黄色的虚线：假定虚线对应的横坐标数值为10%，也就是波动率为10%的情况下，有5条收益曲线符合，其中A点的收益最大（纵坐标数值最高）。如果你是投资者，你必然选择A，因为A点相比于其他点在承受相同的风险情况下，收益最高。以此类推，我们可以在任意给定波动率下找到收益最高的点，将这些点连接起来（一般为曲线），构成的连接线就称之为有效边界（efficient frontier）。
根据此理论建立的有效边界计算器能让你在确定资产种类后，计算出各种配置下的最优解。跟波动率一样，有针对历史数据的有效边界计算器和未来预测的有效边界计算器，如何进行实际操作且听下回分解。
未经允许不得转载：tiger trade » 现代资产组合论（二）——有效边界
