tiger trade此贴紧接上一贴，继续讲收益率。上一贴讲了普通收益率，这次我们讲对数收益率。
普通收益率和对数收益率的区别用一张图就可以简单明了的表示。
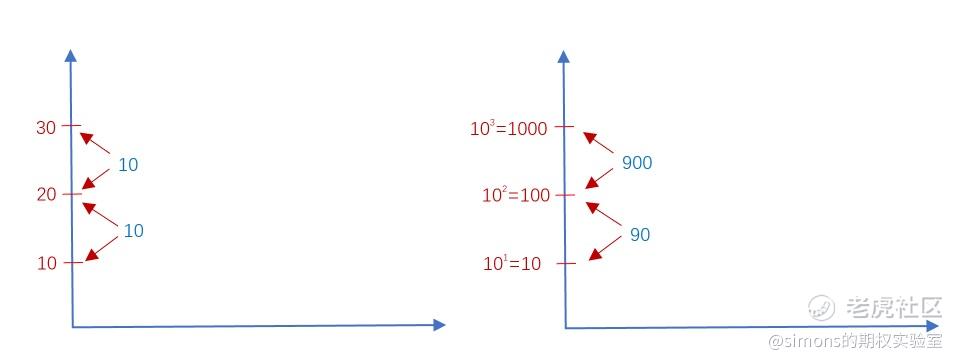
我们可以看出普通收益率的纵坐标（表示收益）是线性的，对数收益率是非线性的。当显示一个长期资产的收益率时，可能是几何级别的增长，这时候就要用对数收益率表示。
对数收益率（log return）：ln（今日收盘价/上一收盘价）（ln是以e为底的求对数）。
累计对数收益率（cumulative log return）：起始日期至计算日之间每天的对数收益率总和。
我们继续读懂你的收益率曲线（二）中的AAPL excel表格为例，在G列、H列增加对数收益率、累计对数收益率2项。其计算公式如图：
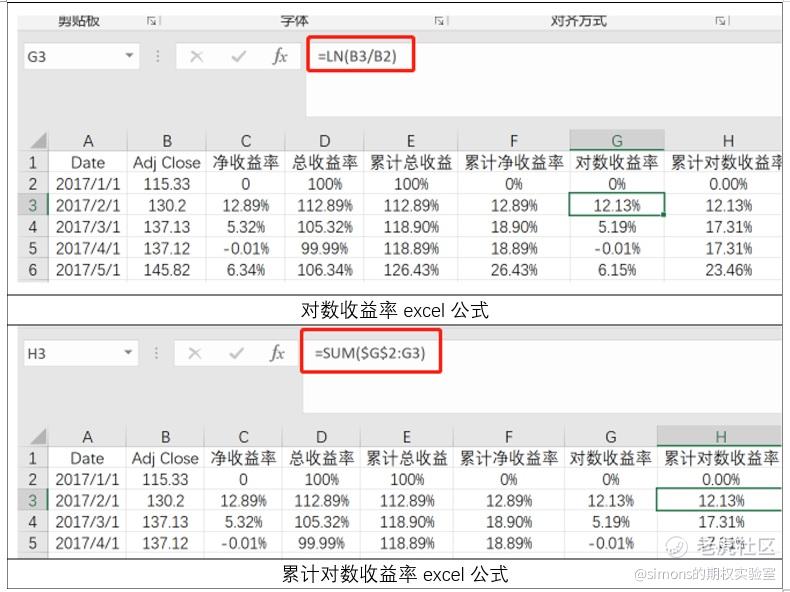
经全部计算对数收益率和累计对数收益率后，我们可以将常规收益率与对数收益率进行对比。我们可以发现2者间的差距很小。
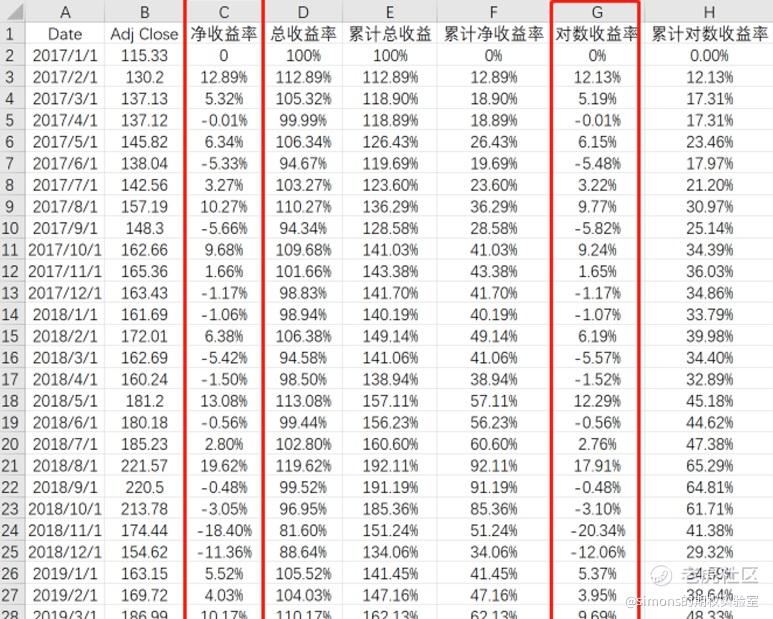
下图揭示了2者之间的关系，从图上可以看出常规收益率和对数收益率在-10%~+10%的区域内基本重合，说明在这区间内2者的差距不大，而且一般股票绝大部分日波动均在-10%~+10%范围内。
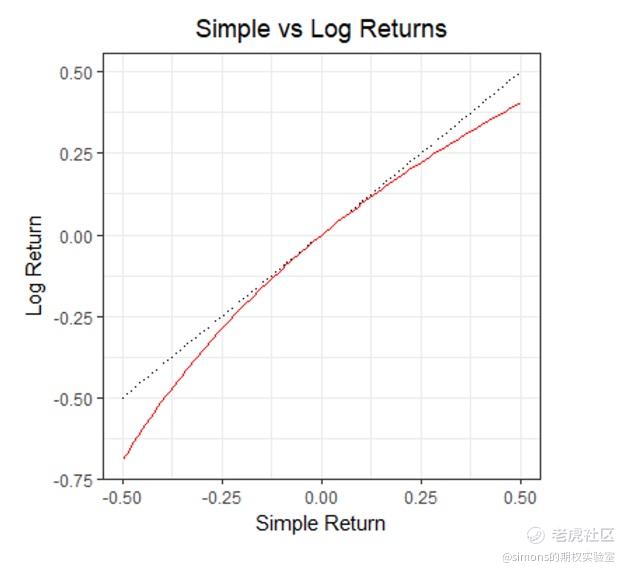
普通收益率与对数收益率转换：
对数收益率=ln（普通收益率+1）
普通收益率=exp（对数收益率）-1
看到这里，有人会问对数收益率有啥用？仅是为了显示方便吗？其实不然。我们回到那个excel表格，列H所代表的累计对数收益率，其计算只要从开始之日起至当天的对数收益率相加即可得出。例如：7月5日的累计对数收益率即为7月1日至7月5日的对数收益率相加。
最后我们计算出后累计对数收益率，用我们投入的金额*exp（累计对数收益率），就能画出《读懂你的收益率曲线（二）》结尾一模一样的资金曲线了。
怎么样，对数收益率的简便计算方法是常规收益率做不到的，常规收益率必须按每天递推来计算累计。用对数收益率在多资产多时期的账户收益率计算非常方便。
未经允许不得转载：tiger trade » 读懂你的收益率曲线（三）——对数收益率
