其实整个系列要讲清楚跟收益率曲线相关的就2个方面:收益率及风险。之前几篇帖子讲完了收益率,接下来我们进入第二部分——风险。风险这边可能要5-10篇帖子,我自己也没想好,一步一步来。但必须要了解清楚的是:风险比收益重要得多得多。我们要做的是连续几十年稳定的盈利而不是一年几十倍第二年输光的赌徒。Okay,接下来是风险的第一章——方差。
我们拿出前几贴的例子AAPL.csv,(这个csv将贯穿整个系列)将A列(日期)、C列(净收益率)选中后生产图表(XY图),将产生下图:
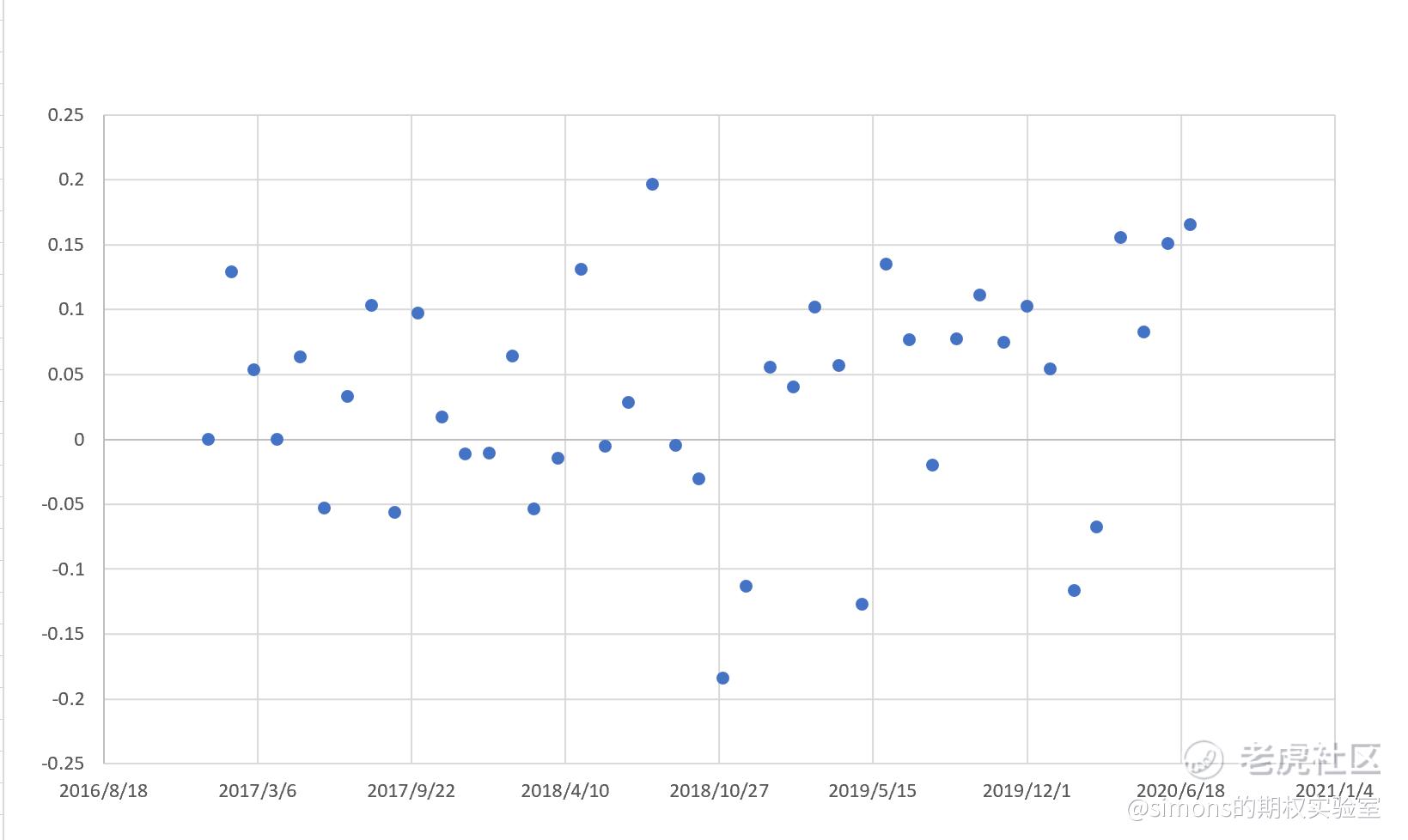
CSV内是我们从雅虎财经截取的2017年1月至2020年7月共43条月数据。图上横坐标是日期、纵坐标是净收益率,每一个点代表一个指定月内的净收益率,共计43个点。
方差测量的图中各点与均值的离散程度。公式为:
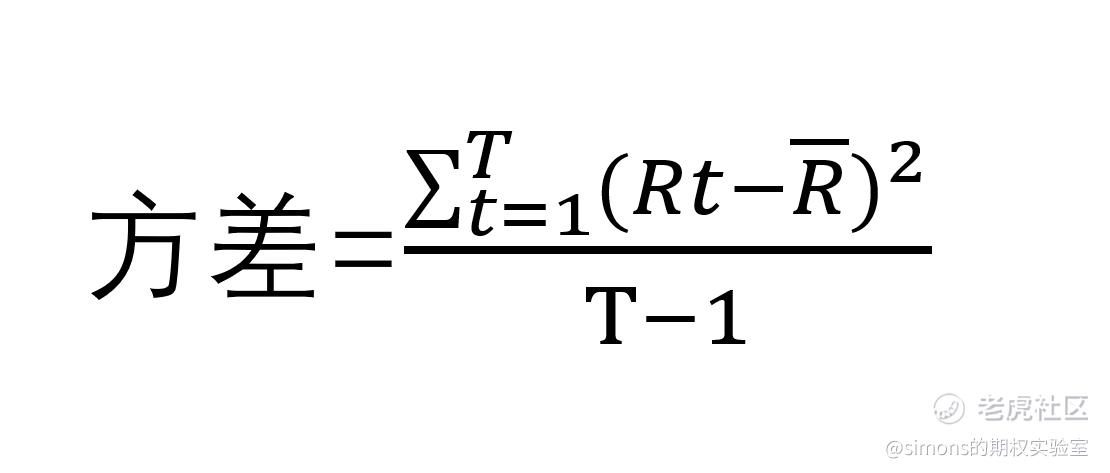
Rt指的是某月的净收益率。
R拔(头上带横线的R)指的是各月净收益率的算数均值。
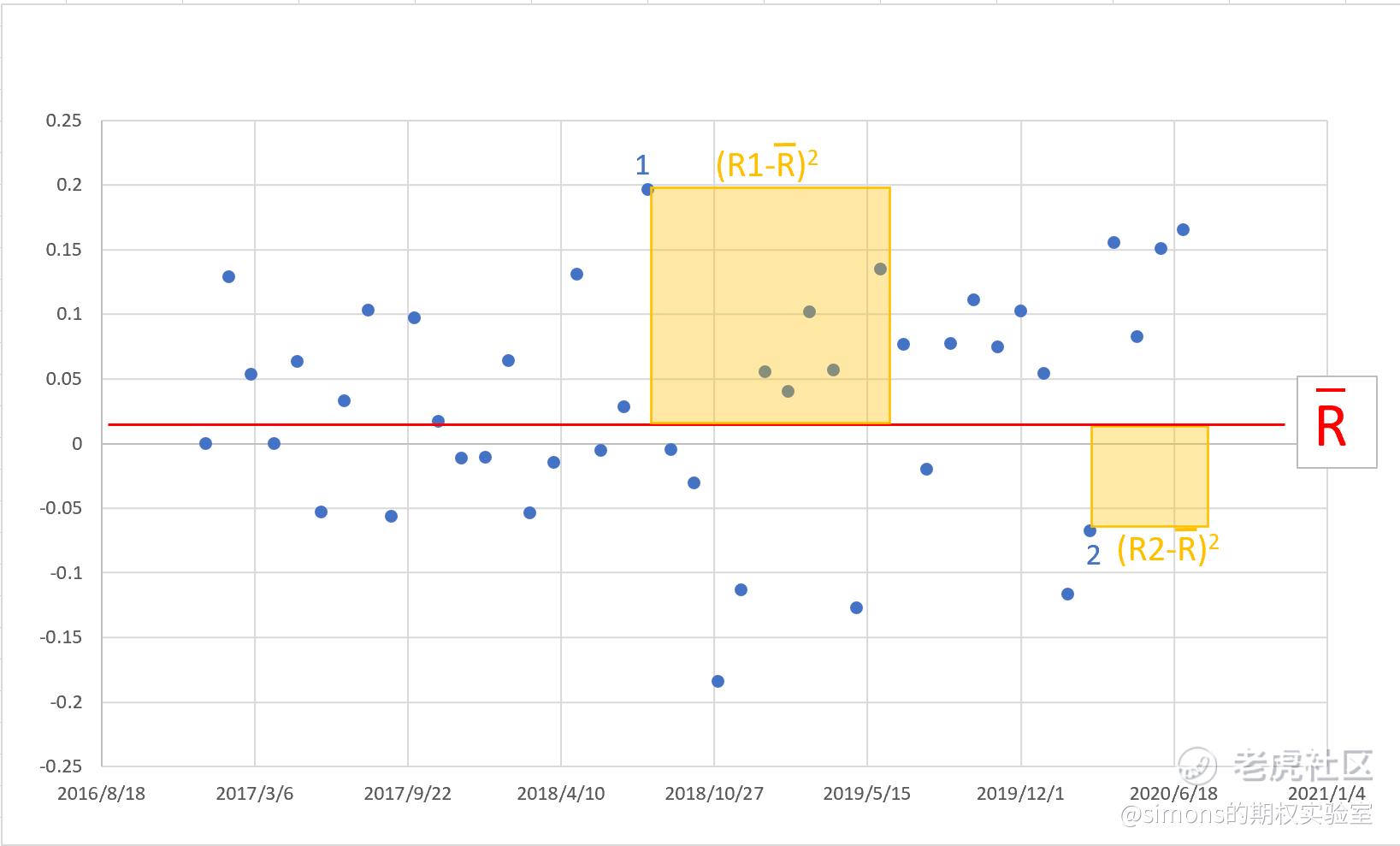
我们从图形上来解释方差的定义。
1、首先我们将43个月的收益率进行算数平均,计算出R平均(均值符号为R头上一横线,如图,因没有该字符,用R平均来表示)。图中以红色横线表示。
2、图上我们选取2个点,点1和点2来说明。先看点1:点1代表的是2018年的8月份,收益为20%左右,是AAPL近些年表现最好的一个月。我们计算该点与R平均的距离(R1-R平均),即该点到红线的垂直距离。然后将该值进行平方,(R1-R平均)^2,即图中大黄色方块的面积。同理对点2也进行类似计算,得出小黄色方块的面积。
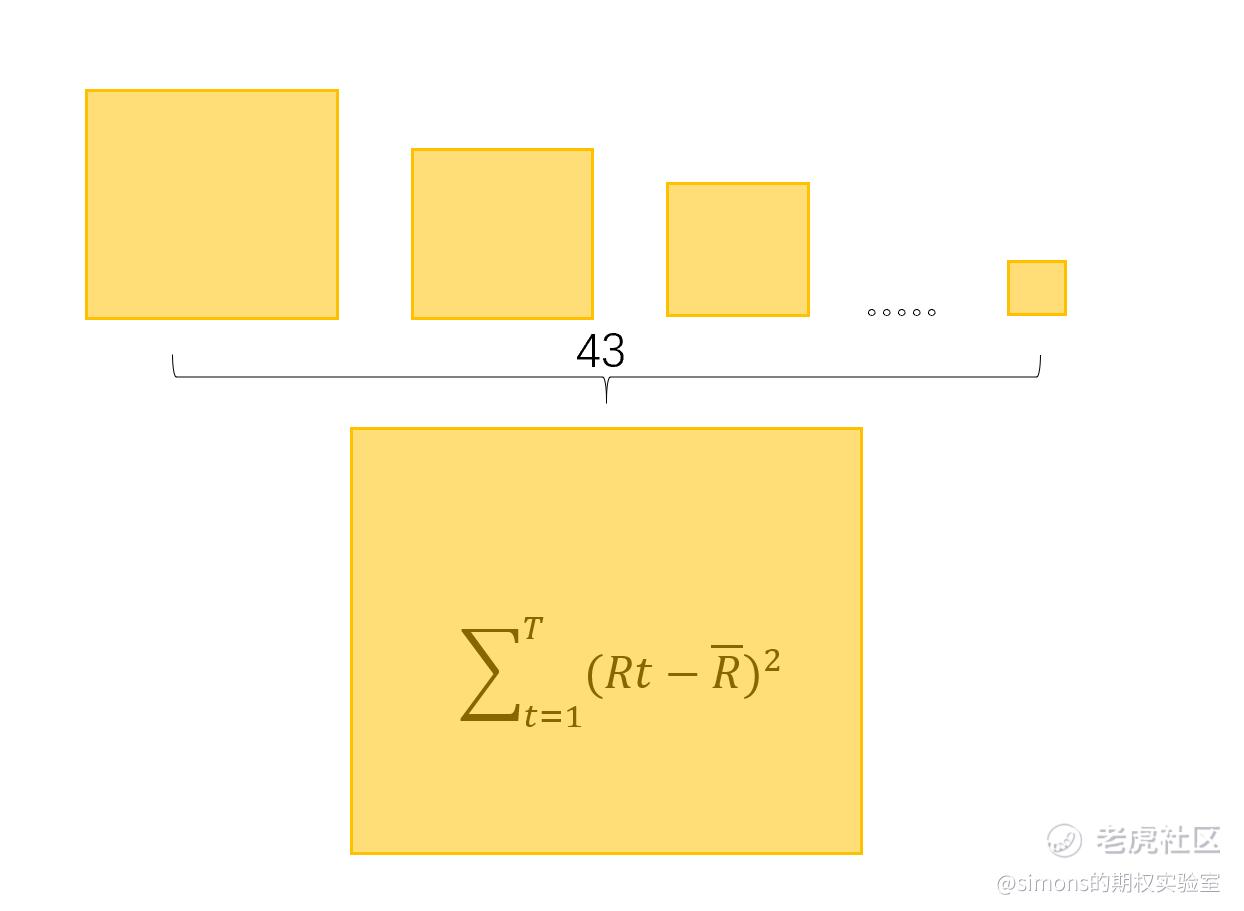
3、以此类推。通过每个点这么计算,可以得出43个正方形,将这些正方形面积相加,得到一个“巨大”的正方形,其面积即为方差公式的分子部分。
4、将“巨大”正方形面积除以(T-1),T为点的数量,例子中为43-1=42,即为方差。
关于方差的几点数学说明:
1、用离均值差距的平方数去表征点位离散程度是方差公式的核心。同时平方数也抵消了收益率有正数有负数的不利情况,平方后永远是正数,统一了度量衡。
2、分母是T-1。因为一个点是无法表征离散程度的。公式确保了样本数必须大于1。
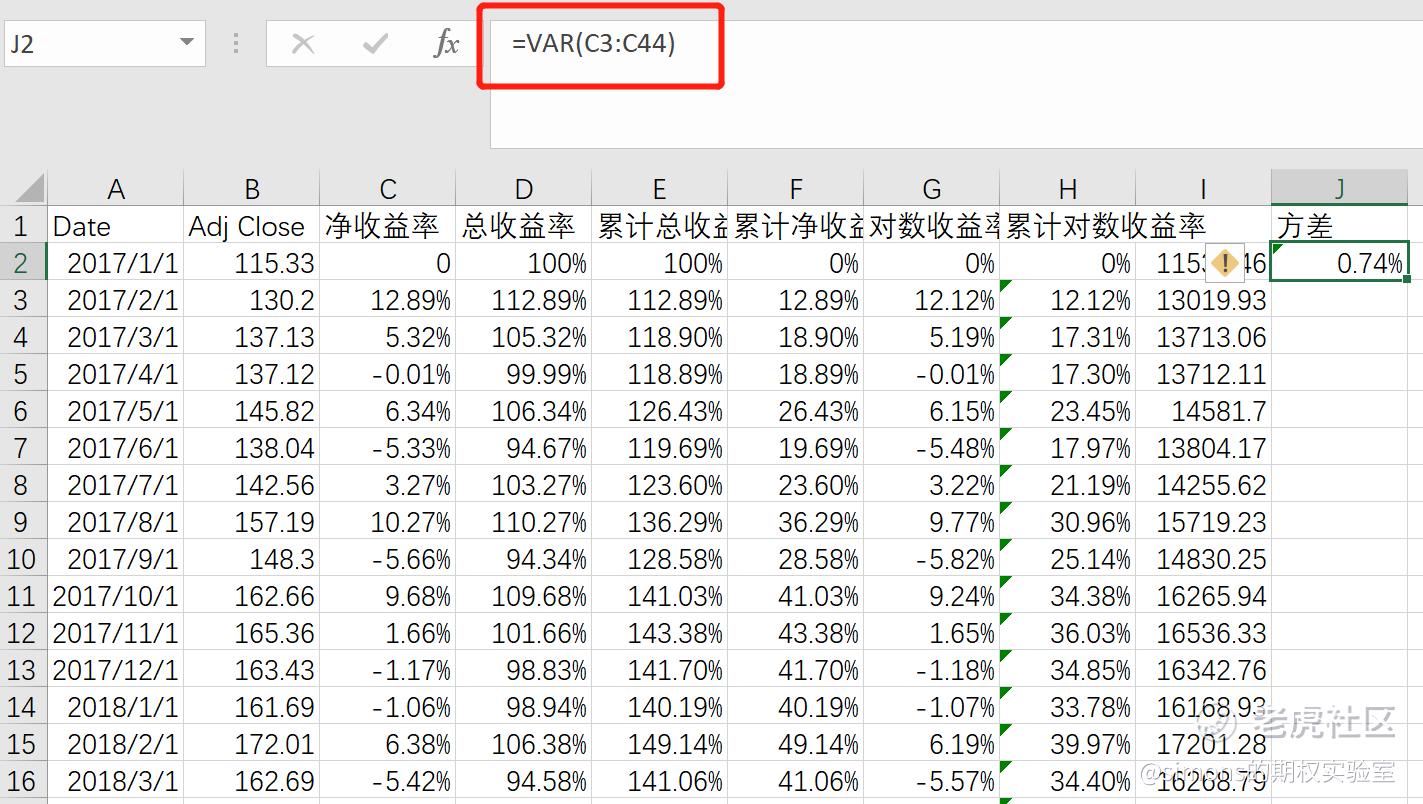
接下来我们回到excel,利用excel内有的函数var,直接下拉净收益率,得出我们月收益率的方差。
未经允许不得转载:美股开户者 » 读懂你的收益率曲线(五)——方差
 美股开户者
美股开户者