收益率曲线读懂你的收益率曲线（四）——复合年化收益率CAGR-tiger trade

一、算数平均与几何平均

在讲CAGR之前，我们先来看2个数学概念：算数平均与几何平均。

简单的举例：有4个数，1,2,3,4

算数平均：（1+2+3+4）/4=2.5

几何平均：（1*2*3*4）^(1/4)=1.8

二、一个实例

举个很简单的例子，如果一个投资者投入1000元买入股票第一年收益率为50%，第二年亏了50%，其资金变化如下：

第一年：1000*1.5=1500元

第二年：1500*0.5=750元期末亏损了250元，根据初始本金算:2年亏损了25%。

那么问题来了：其2年间的年化复合投资收益率为多少？

计算方式1：第一年收益率+50%,第二年收益率为-50%，其总收益率为[(+50%)+(-50%)]/2=0%

计算方式2：根据其期末亏损25%计，分摊到2年：(-25%)/2=-12.5%

第一种计算方法为算数平均计算，明显无法准确表征投资者的损失情况，明明是亏损的，计算出的收益率却为0。

第二种计算可能是我们想象出的“土办法”，其计算出的-12.5%的收益率比较贴合我们心理的数字。

第三种用几何平均来计算：[(1+0.5)+(1-0.5)]^(1/2)-1=-13%。其计算结果与方法2很接近，而且更科学。

三、复合年化收益率CAGR

实际上第三种即为复合年化收益率的计算方式。

复合年化收益率CAGR（Compounded Annual Growth Rate），为一项投资在特定时期内的年度增长率，其使用的是几何平均的算法，这种算法考虑了每年复利的情况，所以更准确。

CAGR公式1：(总收益率1*总收率2****总收益率n)^(1/n)-1

CAGR公式2：(期末余额/初始金额)^(1/n)-1

2个公式均可适用，公式1是从每年的收益率推算，注意这里用的是总收益率，而不是净收益率。公式2是从资金推算。

继续我们的AAPL表格，在I列加入资金，在J1加入CAGR。假定我们于2017年1月1日买入100股AAPL股票，利用读懂你的收益率曲线（三）——对数收益率提到的公式：金额*exp（累计对数收益率）计算出当月资金（I列），利用公式：(期末余额/初始金额)^(1/n)-1计算CAGR（J2单元格）。

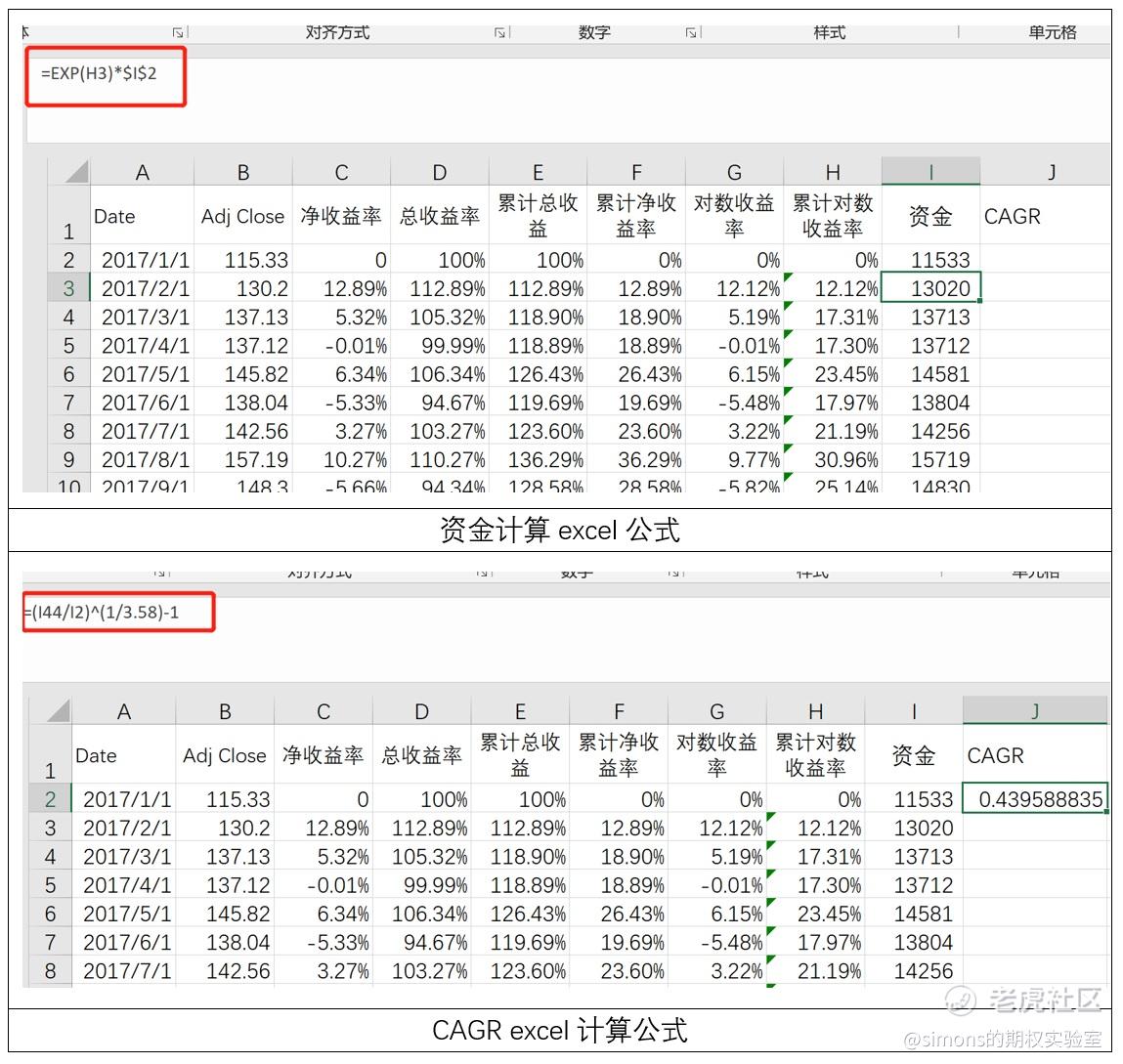
整个excel表格数据为17年1月1日至20年7月31日，折合成年为3.58年，这是CAGR的计算公式内3.58的出处。经过我们计算可以得出：17年买入$AAPL$并一直持有，至今的复合年化收益率为44%。

收益率曲线读懂你的收益率曲线（四）——复合年化收益率CAGR